一道数学趣题
一道数学趣题
在微博上看到一道很有意思的数学问题,原题是:如果椭圆游泳池有一英尺宽的边缘,问:边缘外围是否仍为椭圆? 这个问题背后还有个八卦故事,数学家Steven Strogatz是非线性动力学大师级人物,广为人知的是他和自己的高中数学老师Don Joffray有着深厚的友谊,这位老师是把他带入数学殿堂的引路人,一次他在接受采访时,Strogatz讲到自己和这位老师的故事,他们即使在毕业后也一直保持着联系,一开始是他写信请教老师问题,但转折点就是这个“elliptical pool”问题,老师第一次被问住了,反而是他给老师解释,这令他激动不已。
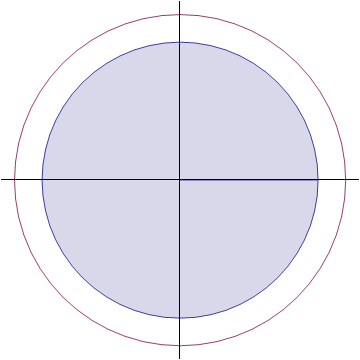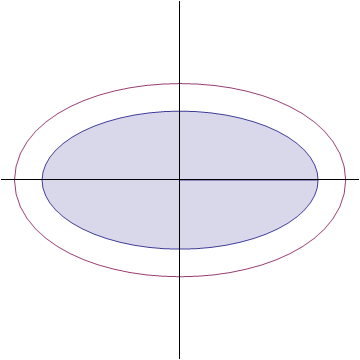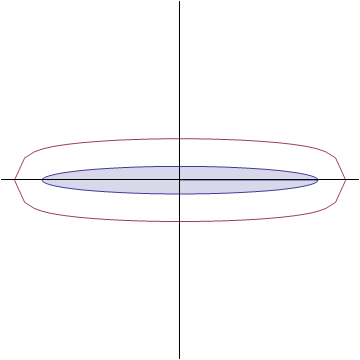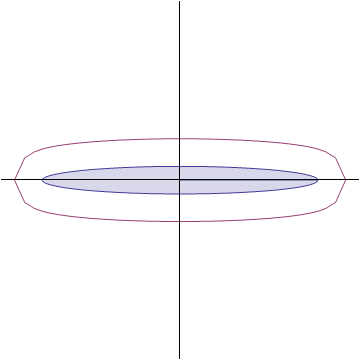
有趣的问题就是这样,看起来足够简单,却要费一番脑筋才能想清楚。这里先定义一个概念,“一英尺宽的边缘”的数学含义,是指在椭圆的每个点的法线方向上扩展一定的长度,微博上另一位博主给出了一个很相像的动态图来描述,这里直接借用一下:
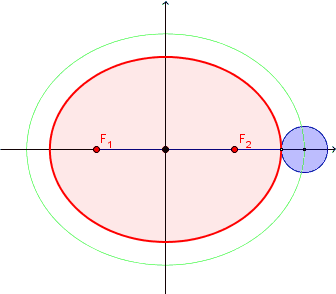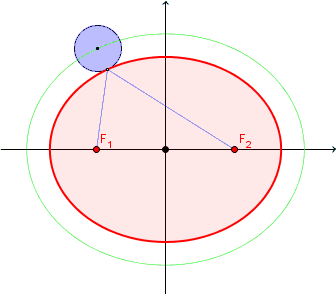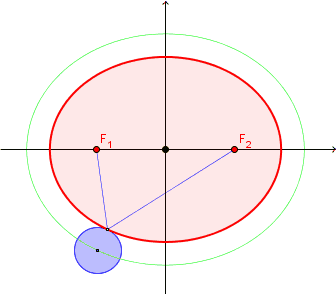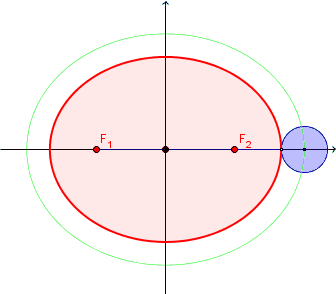
这个问题有两种解决思路,一种是纯粹从数学公式入手,这里给出一个解法,首先对于任意一个椭圆,用参数函数表达:
利用微分知识可知,对于平面上任意一个连续的曲线函数,如果其参数方程表达为
所以对于椭圆上任意一点
假设轮廓的宽度为
如果这个轮廓是一个椭圆的话,那么必然
把公式1代入2中既可发现只有在
当然,如果只是想知道答案的话,可以不用这么麻烦,还有一种思路就是利用极端情况。设想一下这个椭圆极其“扁”,那么它的形状像是两条紧紧贴在一起的线段,不难想象,如果在这个椭圆外扩展一个宽度,那么新的轮廓的的上下边缘类似于两条分开的平行线段,但两端却无法平滑连在一起,这个形状类似于一个圆角的矩形,显然不是椭圆,下面是一个用Mathematica模拟的动态图