如何生成一个随机的圆形
如何生成一个随机的圆形
最近在工作中遇到这么一个问题:
在游戏场景中有一个怪物生成点,这个生长点产生的怪物均匀分布在半径为R的圆形内,这个随机算法应该如何生成?看起来很简单,随手写了一个:
#define RAND ((float)rand()/RAND_MAX)
void get_random_pos(float center_x, float center_y, float radius, float&x, float& y)
{
float u = RAND*radius;
float v = RAND*2*PI;
x = center_x + u*cos(v);
y = center_y + u*sin(v);
}但写的过程中,直觉告诉我,这么写肯定是有问题的,试想,如果以北京为例,如果北京的人口是均匀分布的,那么如果让所有人都报出自己家和天安门的距离,那么这些数据肯定不是均匀,因为居住在五环附近的人数肯定要大于居住在二环附近的人数,于是用Mathamatica实验一下:

果然,这么写是不对的,网上查了一下,这个问题还真是有人研究过,说应该把所获得的随机数开平方一下,实验一下:

但是,这个开平方背后的数学原理究竟是什么呢?抽空翻了下概率书,原来,其中的道理并不复杂,这里涉及到概率里的一个基本概念,累计分布函数(Cumulative distribution function),简称CFD,它的定义如下:
设有一个随机变量
以最为常见的均匀分布概率为例,设均匀分布的随机变量
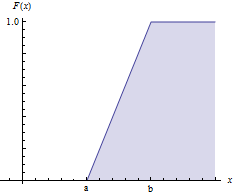 | |
对于一个累计分布函数,符合以下规律
回到我们的问题中,假设怪物产生的范围的半径为
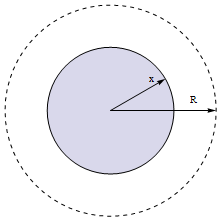
也就是说
现在我们手头上只有均匀概率的随机数产生器,要想产生这么个随机数需要用到一个很巧妙的运算,就是反函数。设随机变量
证明如下
初看起来有点复杂,其实在下面的图上可以很直观的理解这个过程:
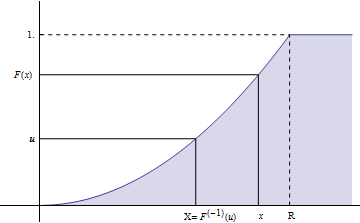
这是利用了
所以最终的算法可以写成
#define RAND ((float)rand()/RAND_MAX)
void get_random_pos(float center_x, float center_y, float radius, float&x, float& y)
{
float u = sqrt(RAND)*radius;
float v = RAND*2*PI;
x = center_x + u*cos(v);
y = center_y + u*sin(v);
}