如何计算线段和圆的交点
如何计算线段和圆的交点
一个程序里用到了计算线段和圆相交情况的算法,在这里记下来备忘
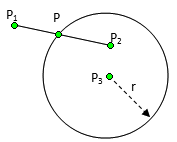
设线段的两个端点分别是
其中,
由于P也在圆上,所以
联立上面的公式,可以得到
其中
解一元二次方程,可以得到
根据
- 如果小于0,表示没有交点
- 如果等于0,表示相切,只有一个交点
- 如果大于0,表示有两个交点
针对
- 如果线段和圆没有交点,而且都在圆的外面的话,则
- 如果线段和圆没有交点,而且都在圆的里面的话,
- 如果线段和圆只有一个交点,则
- 如果线段和圆有两个交点,则
- 如果线段和圆相切,则