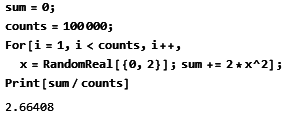比如扔一个质地均匀的色子,产生的结果就是一个离散随机变量,,离散随机变量中的每一个可能的值都对应一个概率,对于扔色子这个例子,,所有离散随机数值的概率之和为
计算机中产生一个[0,1]之间的随机函数rand(),在不考虑浮点数精度时,就是一个连续的随机变量
衡量一个随机数的概率分布规律的两个重要函数,概率分布函数(cumulative distribution function)用来定义概率累计的结果
其中函数表示某事件发生的概率,也就是说表示随机变量小于的概率
比如对于一个在[a,b]之间概率均匀分布的随机变量
特别的,一个在[0,1]之间均匀分布的随机变量的概率分布函数
- 为单调上升的右连续函数
对于连续性随机变量,其概率分布函数可以表达成函数的积分
称为随机变量的概率密度函数,可以理解为随机变量出现在区间之间的概率为
对于均匀分布在[a,b]之间的随机变量,有
正态分布
对于离散随机变量,定义期望值
对于连续型随机变量,定义期望值
比如对于扔色子的结果
对于标准正态分布
如果是常量,那么
对于随机变量,获取其序列值,当时,其平均值趋近于期望值
想求一个函数在[a,b]区间的定积分
定义一个随机数序列,在[a,b]区间的概率密度函数为,定义
那么序列也是一组随机数序列,其期望值
根据大数定理
所以
比如需要计算
设随机变量在[0,2]区间均匀分布,那么,那么
用Mathmatica模拟
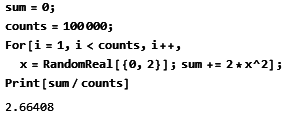
计算机中生成的随机数一般是概率均匀分布的随机变量,一般用表示均匀分布在[0,1]之间的随机变量,如果一个随机变量的概率密度函数为,概率分布函数为,那么产生随机变量的采样函数为概率分布函数的反函数
随机变量有一个很重要的特性
随机变量的概率的分布函数肯定是单调递增函数,所以它的反函数也一定是单调递增函数,所以
比如想产生一个随机点,均匀分布在一个半径为R的圆内,设产生的随机点的极坐标为,那么的概率分布函数
所以产生随机点的采样函数为