匀速贝塞尔曲线运动的实现(一)
匀速贝塞尔曲线运动的实现(一)
贝塞尔曲线(Bézier curve)是一种常用的曲线,以最简单的二次贝塞尔曲线为例,通常以如下方式构建,给定二维平面上的固定点
用一个动画来演示,可以更加清楚的表明这条曲线的构建过程
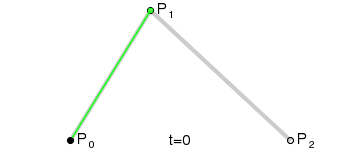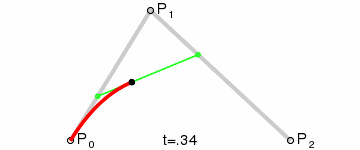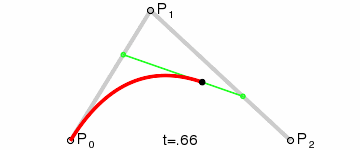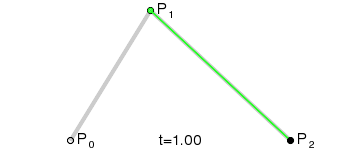
如果
可以看出中间的点较为密集,而两边则较为稀疏。
如何得到匀速的贝塞尔曲线运动呢?比如我们在某款游戏中设计了一条贝塞尔曲线的路径,如何实现NPC匀速在这条路径上运动?
首先需要求得
为了简化公式,定义如下变量
计算出
根据这个公式,求得贝塞尔曲线的长度公式
特别当
设
也就是
视
根据牛顿切线法,求解
由于
上面是使用javascript实现的互动曲线,核心代码如下
class QuadBezierLine {
constructor(_p0, _p1, _p2, _step, _uniformSpeedMode) {
this.step=_step;
this.points=[];
this.uniformSpeedMode=_uniformSpeedMode;
this.updatePoints(_p0, _p1, _p2);
}
//Speed(t_) = Sqrt[A*t*t+B*t+C]
speed(t) {
return Math.sqrt(this.A * t * t + this.B * t + this.C);
}
//Length(t) = Integrate[Speed[t], t]
//Length(t_) = ((2*Sqrt[A]*((2*A*t + B)*Sqrt[A*t^2 + B*t + C] - B*Sqrt[C]) +
// (B^2 - 4*A*C)*(Log[B + 2*Sqrt[A]*Sqrt[C]] -
// Log[B + 2*A*t + 2*Sqrt[A]*Sqrt[A*t^2 + B*t + C]]))/(8*A^(3/2)))
length(t) {
let temp1 = Math.sqrt(this.C + t * (this.B + this.A * t));
let temp2 = (2 * this.A * t + this.B) * temp1 - this.B * Math.sqrt(this.C);
let temp3 = Math.log(this.B + 2 * Math.sqrt(this.A * this.C));
let temp4 = Math.log(this.B + 2 * this.A * t + 2 * Math.sqrt(this.A) * temp1);
let temp5 = 2 * Math.sqrt(this.A) * temp2;
let temp6 = (this.B * this.B - 4 * this.A * this.C) * (temp3 - temp4);
return (temp5 + temp6) / (8 * Math.pow(this.A, 1.5));
}
//u'=u-(Length(u)-len)/Speed(u)
invertLength(u0, len) {
let u1 = u0, u2;
do {
u2 = u1 - (this.length(u1) - len) / this.speed(u1);
if (Math.abs(u1 - u2) < 0.000001)
break;
u1 = u2;
} while (true);
return u2;
}
updatePoints(_p0, _p1, _p2) {
this.p0=_p0;
this.p1=_p1;
this.p2=_p2;
let ax = this.p0.x - 2 * this.p1.x + this.p2.x;
let ay = this.p0.y - 2 * this.p1.y + this.p2.y;
let bx = 2 * this.p1.x - 2 * this.p0.x;
let by = 2 * this.p1.y - 2 * this.p0.y;
this.A = 4 * (ax * ax + ay *ay);
this.B = 4 * (ax * bx + ay *by);
this.C = bx * bx + by * by;
this.points.length = 0;
let totalLength = this.length(1);
for (let index = 1; index < this.step; index++) {
let t = index / this.step;
if(this.uniformSpeedMode) {
t = this.invertLength(t, totalLength*t);
}
let x = (1-t)*(1-t)*this.p0.x+2*(1-t)*t*this.p1.x+t*t*this.p2.x;
let y = (1-t)*(1-t)*this.p0.y+2*(1-t)*t*this.p1.y+t*t*this.p2.y;
this.points.push({x:x, y:y});
}
}
draw() {
this.points.forEach(pt => {
fill('green');
ellipse(pt.x, pt.y, 5, 5);
});
}
}