匀速贝塞尔曲线运动的实现(二)
匀速贝塞尔曲线运动的实现(二)
实际工程应用中最为常见的是三次贝塞尔曲线,也就是下面这种用4个控制点生成的曲线
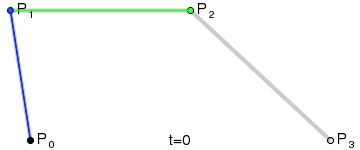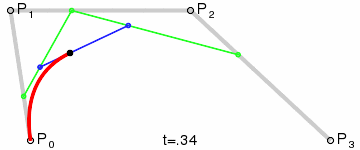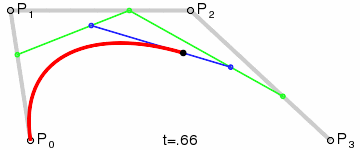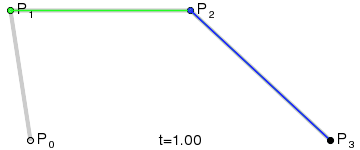
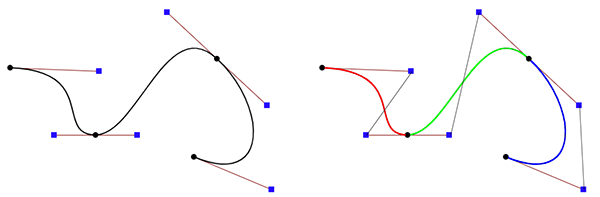
三次贝塞尔曲线的一个方便之处在于可以将相邻的两个控制点之间的连线视作控制点的“切线”,进而便于使用者编辑,因此在很多软件中的贝塞尔曲线编辑器都是使用的三次贝塞尔曲线。比如下面这段曲线,其实就是由几段三次贝塞尔曲线组成的。
三次贝塞尔曲线的公式为:
虽然仍然可以按照相同的思路去实现匀速运动,但是由于三次贝塞尔曲线的长度计算已经非常复杂,根本无法通过对速度进行积分得到解析解,更别说通过反函数去求解匀速需要的自变量了。 因此在实际计算中,一般也只能通过提前建立一个曲线的长度查询表辅助运算。 这个长度查询表可以利用一般的数值积分的方式建立,比如辛普森积分法
下面是一个JavaScript实现的互动范例,代码可以直接查看这个页面的JS源码