BRDF(双向反射分布函数)

1. 物体对光的反应

1.1 金属

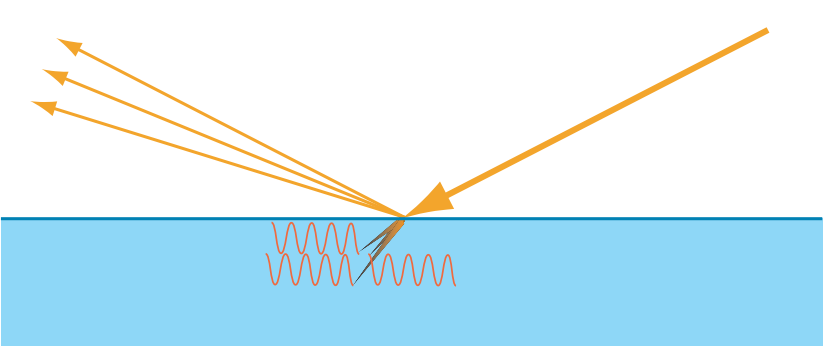
对于金属，折射进表面的光线的能量会立即被金属中的自由电子吸收，转换成电子的能量，不再可见

1.2 非金属

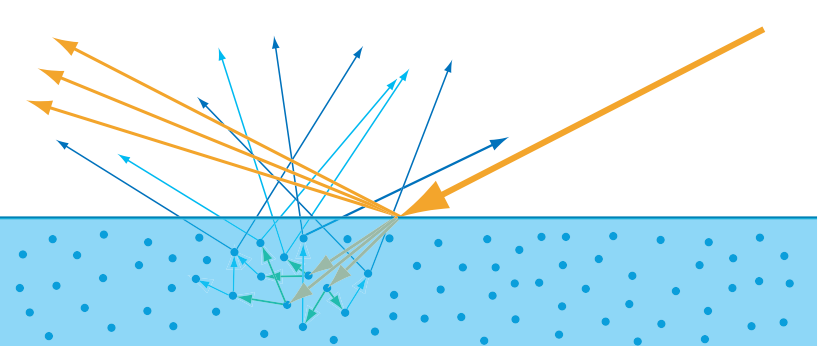
对于非金属（电介质或绝缘体），它们往往不是由单一成分构成，而可以认为其中包含了很多折射率不同的微粒，光线遇到这些粒子后发生反射折射，在物质内部不断传播，散射到不同方向，其中一部分会再次穿过表面被观察到,这种现象称为次表面散射(Subsurface Scattering)

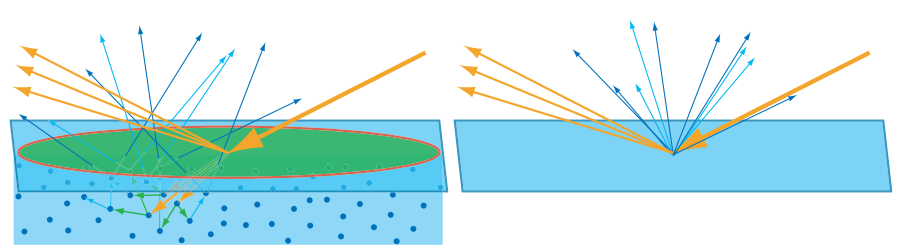
如果光线在物质中传播距离小于观察尺度（绿色区域，可以认为是一个像素区域），我们看到情况如下面的右上图，入射点、反射点、次表面散射的出射点看起来是同一个点。其中反射部分（图中浅棕色出射光）就是我们常说的高光（Specular Light），常聚集在一个方向周围，向这个方向观察该点会看到明显的高光，从其他方向观察该点时高光则比较微弱；次表面散射部分（图中蓝色出射光）是漫射光（Diffuse Light），光线被散射到各个方向。

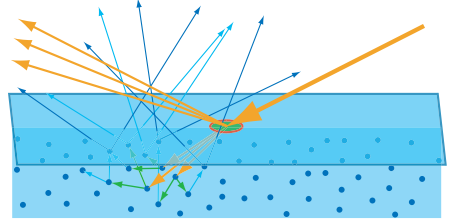
如果光线在物质中的传播距离大于观察尺度，就需要使用次表面散射算法来建模

2. BRDF

2.1 定义

BRDF(bidirectional reflectance distribution function),是用来描述反光小平面的反射光和入射光的比例关系的函数，设一个不透明的、不发光的小平面，BRDF的定义为

f (\vec{ω_{i}}, \vec{ω_{o}}) = \frac{d L_{o} (\vec{ω_{o}})}{d E_{i} (\vec{ω_{i}})}

其中 $f$ 就是BRDF函数 $\vec{ω_{i}}$ 是入射光方向， $\vec{ω_{o}}$ 是观察方向 $L_{o} (\vec{ω_{o}})$ 是 $\vec{ω_{o}}$ 方向反射光的亮度(Luminance) $E_{i} (\vec{ω_{i}})$ 是小平面接受的照度在 $\vec{ω_{i}}$ 方向上的分量, 由照度和亮度的定义可知，来自入射方向的入射光的辐射率（亮度）为

L_{i} (\vec{ω_{i}}) = \frac{d Φ}{d ω_{i} d A^{P r o j}} = \frac{d Φ}{d ω_{i} d A \cos θ_{i}} = \frac{d E (\vec{ω_{i}})}{d ω_{i} \cos θ_{i}}

得到 $d E_{i} (\vec{ω_{i}}) = L_{i} (\vec{ω_{i}}) \cos θ_{i} d ω_{i}$ ，所以

f (\vec{ω_{i}}, \vec{ω_{o}}) = \frac{d L_{o} (\vec{ω_{o}})}{L_{i} (\vec{ω_{i}}) \cos θ_{i} d ω_{i}}

2.2 特性

\begin{aligned} f (\vec{ω_{i}}, \vec{ω_{o}}) & \geq 0 \\ f (\vec{ω_{i}}, \vec{ω_{o}}) & = f (\vec{ω_{o}}, \vec{ω_{i}}) \\ \forall \vec{ω_{i}}, \int_{Ω} f (\vec{ω_{i}}, \vec{ω_{o}}) \cos θ_{o} d ω_{o} & \leq 1 \end{aligned}

2.3 为什么BRDF方程是L和E的比值

参考

2.3.1 从测量方面来看

测量入射光的设备测量小平面的照度（E）最方便，不用关心方向，而测量出射光则是测量辐射率(L)最方便，用狭长的测光筒

2.3.2 从数学角度来解释

一束光照到平面后，被平面反射到各个方向，其中一个出射方向的光通量只是整个反射光通量极小的一部分，当出射方向立体角趋于0时，

lim_{ω_{o} \to 0} \frac{d L_{o}}{L_{i}} = 0

所以在实际计算中使用辐射率和辐射率比值是没有意义的。而如果分母改成表面上接收到的来自光源方向的微分辐照度， $d E = L_{i} (l) d ω \cos θ_{i}$ ， $d E$ 会小很多，所以比值 $d L_{o} / d E_{i}$ 是有意义的