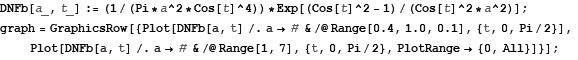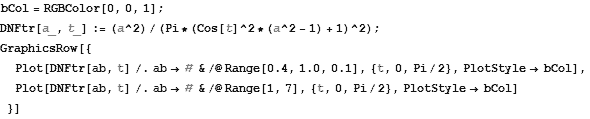所有的法线分布函数都应该符合以下约束
可以理解为,这些为平面在某个指定方向上的投影面积,等于整体宏平面的投影面积

当时,有
Phong模型认为,反射强度正比于,其中表示材质的“光滑程度”,当,材质是绝对的漫反射材质,当,材质成为绝对光滑的镜面,设
由上面法线分布函数的归一性可知
由于
可以得到最终D函数为
一般引擎用粗糙度(取值范围[0,1])表示材质的光滑程度,Phong模型中的常用如下公式计算
用Mathmatica绘制函数图


Beckmann的法线分布函数为
经过积分计算,所以
Beckmann法线分布函数中,同样代表了材质的粗糙度,趋向于0时表示绝对光滑,取值却大约粗糙,但当取值超过1时,材质会变得“超级粗糙”(诡异),用如下公式获取
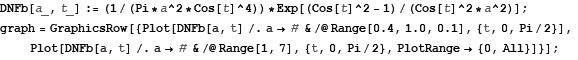

当取值在0.5以下时,Beckmann模型和Phong模型的结果非常相似,这两个参数可以有如下对应关系


这个模型又被称为GGX模型,是UnrealEngine采用的法线分布函数
经过积分,所以
在Mathmatica中的模拟
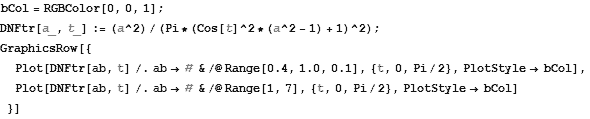

可以看出,当趋向于0,表示材质越光滑,当时,GGX称为一条直线,也就是纯粹的漫反射材质,当,GGX模型的表现类似于Beckmann,表现出“超级粗糙”特性。
和Phong模型比较,可以看出在粗糙度小于0.4时,ggx和phong模型比较类似,当粗糙度大于0.4时,ggx的表现更“平顺”一些,高光中心更集中,但长尾区域更长。


在Unreal实现中,定义了, roughness是用户输入的材质粗糙度,范围在[0,1]之间