几何变换(四）

8. 视图变换管线概览

一个物体从独立的物体最终转换为2D图像，期间经过如下坐标变换

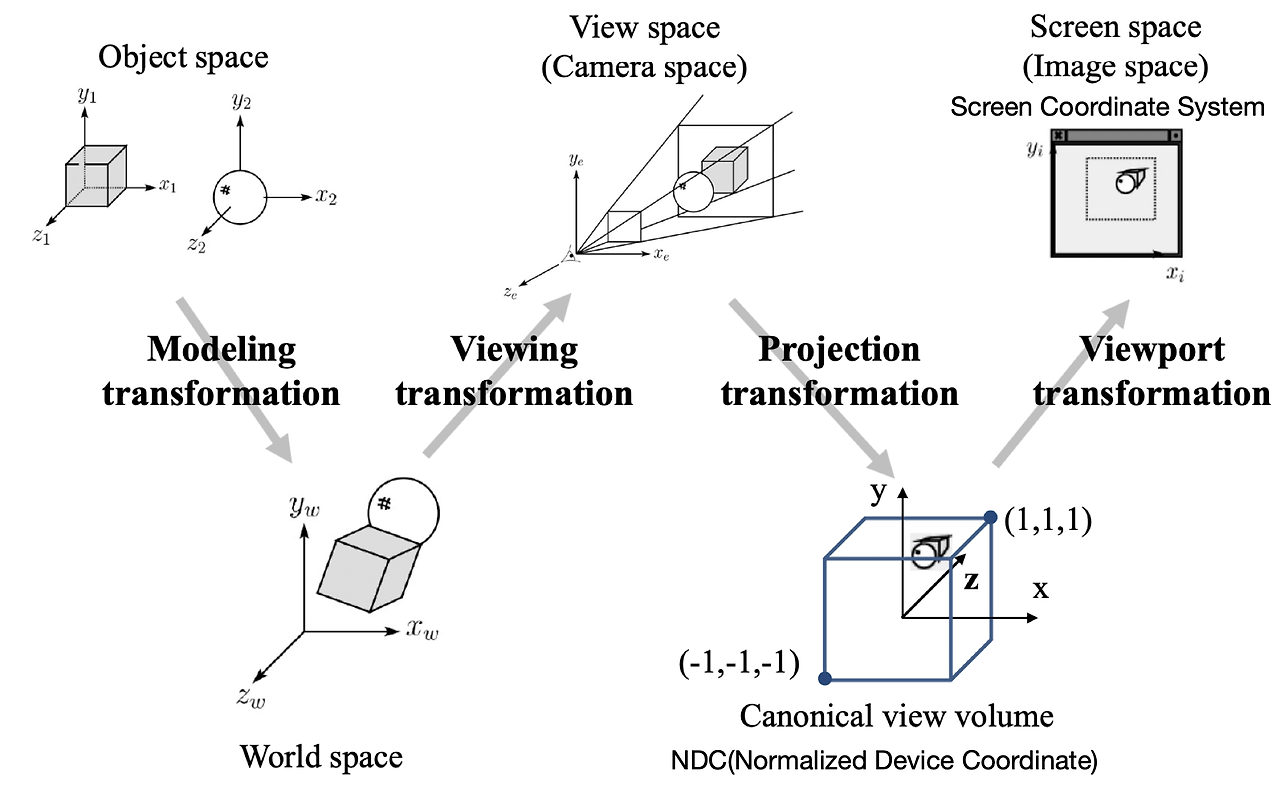
Modeling transformation: 由局部坐标系(Local Space)转换为世界坐标系(World Space)
Viewing transformation: 由世界坐标系(World Space)转换为摄像机坐标系(View Space)
Projection transformation: 由摄像机坐标系（View Space)转换为标准设备坐标系NDC(Normalized Device Coordinate)
Viewport transformation: 由NDC坐标系转换为视口坐标系(Screen coordinate System)

9. 摄像机视图变换（Viewing/Camera Transformation)

9.1 定义

视图变换是将物体的世界坐标系转换到摄像机的坐标系

摄像机坐标系以观察点(eye)为原点，向前方向为-z轴，x轴指向右侧（右手坐标系）所以

\begin{aligned} {\vec{z}}^{'} & = e y e - l o o k a t \\ {\vec{x}}^{'} & = \vec{u p} \times {\vec{z}}^{'} \\ {\vec{y}}^{'} & = {\vec{z}}^{'} \times {\vec{x}}^{'} \end{aligned}

9.2 计算

根据坐标系变换公式，设摄像机在世界坐标系中的位置为 $e$ ，摄像机的三个轴的单位轴向量为 $\vec{i^{'}}, \vec{j^{'}}, \vec{k^{'}}$ 视图变换矩阵为

M_{v i e w} = [\begin{matrix} i_{x}^{'} & i_{y}^{'} & i_{z}^{'} & - \vec{e} \cdot {\vec{i}}^{'} \\ j_{x}^{'} & j_{y}^{'} & j_{z}^{'} & - \vec{e} \cdot {\vec{j}}^{'} \\ k_{x}^{'} & k_{y}^{'} & k_{z}^{'} & - \vec{e} \cdot {\vec{k}}^{'} \\ 0 & 0 & 0 & 1 \end{matrix}]

10. 透视投影变换(Perspective Projective Transformations)

投影变换是将物体从摄像机坐标系转换到标准设备坐标系(NDC)，也就是坐标值在一个 $[- 1, 1]^{3}$ 的盒子里(Canonical view volume) 可以将这个过程分为两步，首先构造一个坐标转换，将摄像机的摄影范围构成的视锥体(Frustum)变形成一个立方体(Cuboid)，然后再将这个立方体转化为成标准设备坐标系下(NDC)的标准观察体CCV(Canonical View Volume)

NDC坐标系在不同的系统上有不同的约定，在DirectX中，近平面到远平面映射到 $[0, 1]$ ，在OpenGL则是把近平面到远平面映射到 $[- 1, 1]$ ，但一般都把NDC坐标系设为左手坐标系。

10.2 求解过程

10.2.1 从视锥体到立方体

设摄像机坐标系中的点 $p (x, y, z)$ ，转换后的坐标为 $(x^{'}, y^{'}, z^{'})$ ，由定义可知 $p$ 投影到摄像机近裁剪面上的点为 $p^{'} (x^{'}, y^{'})$ ，由相似三角形可知

\begin{aligned} y^{'} & = \frac{n y}{z} \\ x^{'} & = \frac{n x}{z} \end{aligned}

设这个转换矩阵为 $M_{persp \to ortho}$ , 可知

M_{persp \to ortho} [\begin{matrix} x \\ y \\ z \\ 1 \end{matrix}] = [\begin{matrix} \frac{n x}{z} \\ \frac{n y}{z} \\ z^{'} \\ 1 \end{matrix}]

对于表示一个点的其次坐标，所有数值乘以一个同样的数，所表达的意义相同，所以 $[n x / z, n y / z, z^{'}, 1] = [n x, n y, z^{'} z, z]$ ，这里先暂时忽略 $z$ 轴，可以得到

M_{persp \to ortho} [\begin{matrix} x \\ y \\ z \\ 1 \end{matrix}] = [\begin{matrix} n x \\ n y \\ ? \\ z \end{matrix}]

由此可以推断出，这个矩阵的第1，2和4行

[\begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \end{matrix}] [\begin{matrix} x \\ y \\ z \\ 1 \end{matrix}] = [\begin{matrix} n x \\ n y \\ ? \\ z \end{matrix}]

考虑特殊情况，近平面上的任意一点 $[x, y, n]$ 经过这个矩阵转换后

[\begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \end{matrix}] [\begin{matrix} x \\ y \\ n \\ 1 \end{matrix}] = [\begin{matrix} n x \\ n y \\ ? \\ n \end{matrix}]

由于近平面上的点经过转换后坐标不变，所以 $[n x, n y, ?, n] = [x, y, n, 1]$ ，而 $[x, y, n, 1]$ 作为其次坐标，所有数值都乘以 $n$ ，可以得到 $[x, y, n, 1] == [n x, n y, n^{2}, n]$ ，所以

[\begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \end{matrix}] [\begin{matrix} x \\ y \\ n \\ 1 \end{matrix}] = [\begin{matrix} n x \\ n y \\ n^{2} \\ n \end{matrix}]

同理，远平面上的任意一个点 $[x, y, f, 1]$ 转换后为 $[x^{'}, y^{'}, f, 1]$ ，可以得到

[\begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \end{matrix}] [\begin{matrix} x \\ y \\ f \\ 1 \end{matrix}] = [\begin{matrix} x^{'} \\ y^{'} \\ f^{2} \\ n \end{matrix}]

由此可知，第三行的数值和 $x, y$ 无关，一定是形如 $[0, 0, A, B]$ 这样的形式，且

\begin{array}{r} A n + B = n^{2} \\ A f + B = f^{2} \end{array}

可以得到

\begin{aligned} A & = f + n \\ B & = - n f \end{aligned}

得到这个转换矩阵为

M_{persp \to ortho} = [\begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & f + n & - n f \\ 0 & 0 & 1 & 0 \end{matrix}]

10.2.2 从立方体到标准观察体

这一步相对简单很多，只要将观察体的中心的 $z$ 挪到原点，做一定的放缩，并且将 $z$ 轴反转即可

\begin{aligned} M_{ortho \to cvv} & = [\begin{array}{c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}] [\begin{array}{c} 2 / w & 0 & 0 & 0 \\ 0 & 2 / h & 0 & 0 \\ 0 & 0 & 2 / (n - f) & 0 \\ 0 & 0 & 0 & 1 \end{array}] [\begin{array}{c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & - (n + f) / 2 \\ 0 & 0 & 0 & 1 \end{array}] \\ = [\begin{array}{c} 2 / w & 0 & 0 & 0 \\ 0 & 2 / h & 0 & 0 \\ 0 & 0 & - 2 / (n - f) & (n + f) / (n - f) \\ 0 & 0 & 0 & 1 \end{array}] \end{aligned}

10.2.3 合并后的矩阵

最终得到合并后的投影矩阵为

\begin{aligned} M_{persp \to cvv} & = M_{ortho \to cvv} M_{persp \to ortho} \\ = [\begin{array}{c} \frac{2 n}{w} & 0 & 0 & 0 \\ 0 & \frac{2 n}{h} & 0 & 0 \\ 0 & 0 & - \frac{n + f}{n - f} & \frac{2 n f}{n - f} \\ 0 & 0 & 1 & 0 \end{array}] \end{aligned}

在大部分工程项目中，摄像机的输入参数一般是如下几个

宽高比 $a s p e c t = w / h$
视场角fov， $\tan (f o v / 2) = - h / 2 n$
近裁剪距离 $n e a r = | n | = - n$
远裁剪距离 $f a r = | f | = - f$

将这些值带入上面的公式，可以得到

M_{persp \to cvv} = [\begin{matrix} \frac{- 1}{aspect . \tan (f o v / 2)} & 0 & 0 & 0 \\ 0 & \frac{- 1}{\tan (f o v / 2)} & 0 & 0 \\ 0 & 0 & - \frac{n e a r + f a r}{n e a r - f a r} & \frac{- 2 n e a r . f a r}{n e a r - f a r} \\ 0 & 0 & 1 & 0 \end{matrix}]

一般来说，当针对一个空间点做矩阵转换时，如果 $M [u_{x}, u_{y}, u_{z}, 1]^{T} = [v_{x}, v_{y}, v_{z}, 1]^{T}$ ，那么

\begin{aligned} (k M) [u_{x}, u_{y}, u_{z}, 1]^{T} & = k [v_{x}, v_{y}, v_{z}, 1]^{T} \\ = [k v_{x}, k v_{y}, k v_{z}, k]^{T} \\ = [v_{x}, v_{y}, v_{z}, 1]^{T} \end{aligned}

可知 $k M$ 在针对空间点转换矩阵中等同于 $M$ ，所以为了表达方便，经常将上面得到的这个矩阵乘以-1，得到

M_{persp \to cvv} = [\begin{matrix} \frac{1}{aspect \cdot \tan (f o v / 2)} & 0 & 0 & 0 \\ 0 & \frac{1}{\tan (f o v / 2)} & 0 & 0 \\ 0 & 0 & \frac{n e a r + f a r}{n e a r - f a r} & \frac{2 n e a r \cdot f a r}{n e a r - f a r} \\ 0 & 0 & - 1 & 0 \end{matrix}]

有时候也会使用Zero-To-One的CVV坐标，也就是z轴是从0到1，这种情况下的转换矩阵为:

M_{persp \to cvv} = [\begin{matrix} \frac{1}{aspect \cdot \tan (f o v / 2)} & 0 & 0 & 0 \\ 0 & \frac{1}{\tan (f o v / 2)} & 0 & 0 \\ 0 & 0 & \frac{f a r}{n e a r - f a r} & \frac{n e a r \cdot f a r}{n e a r - f a r} \\ 0 & 0 & - 1 & 0 \end{matrix}]

10.2.4 深度插值

设摄像机坐标系中有一个线段 $(x_{1}, z_{1}), (x_{2}, z_{2})$ ，在摄像机近平面上的投影为 $(x_{1}^{'}, n), (x_{2}^{'}, n)$ ，线段上有一点为 $(x, z)$ ，投影为 $(x^{'}, n)$ 可知

\begin{array}{r} \frac{x}{x^{'}} = \frac{z}{n} \\ x = \frac{z x^{'}}{n} \end{array}

设线段的方程为 $a x + b z = c$ ，带入可得

\begin{array}{r} a \frac{z x^{'}}{n} + b z = c \\ \frac{1}{z} = \frac{a x^{'}}{c n} + \frac{b}{c} \end{array}

当投影点 $x^{'}$ 在投影线段上线性移动时， $x^{'} = (1 - t) x_{1}^{'} + t x_{2}^{'}$ ，可得

\begin{aligned} \frac{1}{z} & = \frac{a}{c n} ((1 - t) x_{1}^{'} + t x_{2}^{'}) + \frac{b}{c} \\ = (\frac{a x_{1}^{'}}{c n} + \frac{b}{c}) (1 - t) + (\frac{a x_{2}^{'}}{c n} + \frac{b}{c}) t \\ = \frac{1}{z_{1}} (1 - t) + \frac{1}{z_{2}} t \end{aligned}

也就是说，当投影点 $x^{'}$ 在投影线段上线性移动时，原线段上的点的深度值的倒数是线性变换的

\begin{aligned} M_{ortho \to cvv} & = [\begin{array}{c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}] [\begin{array}{c} 2 / (r - l) & 0 & 0 & 0 \\ 0 & 2 / (t - b) & 0 & 0 \\ 0 & 0 & 2 / (n - f) & 0 \\ 0 & 0 & 0 & 1 \end{array}] [\begin{array}{c} 1 & 0 & 0 & - (l + r) / 2 \\ 0 & 1 & 0 & - (t + b) / 2 \\ 0 & 0 & 1 & - (n + f) / 2 \\ 0 & 0 & 0 & 1 \end{array}] \\ = [\begin{array}{c} 2 / (r - l) & 0 & 0 & (l + r) / (l - r) \\ 0 & 2 / (t - b) & 0 & (b + t) / (b - t) \\ 0 & 0 & - 2 / (n - f) & (n + f) / (n - f) \\ 0 & 0 & 0 & 1 \end{array}] \end{aligned}

同理，在工程中一般标注一个正交投影摄像机的主要参数如下

近裁剪距离 $n e a r = | n | = - n$
远裁剪距离 $f a r = | f | = - f$
左侧裁剪面坐标 $l e f t = l$
右侧裁剪面坐标 $l e f t = l$
上侧裁剪面坐标 $t o p = t$
下侧裁剪面坐标 $b o t t o m = t$ 带入上面的公式可以得到

M_{ortho \to cvv} = [\begin{matrix} \frac{2}{r i g h t - l e f t} & 0 & 0 & \frac{l e f t + r i g h t}{l e f t - r i g h t} \\ 0 & \frac{2}{t o p - b o t t o m} & 0 & \frac{b o t t o m + t o p}{b o t t o m - t o p} \\ 0 & 0 & \frac{2}{n e a r - f a r} & \frac{n e a r + f a r}{n e a r - f a r} \\ 0 & 0 & 0 & 1 \end{matrix}]